Matematicas III_iniciales
jueves, 9 de marzo de 2017
miércoles, 9 de noviembre de 2016
Problemas de ecuacion de la recta
PROBLEMAS ECUACIÓN DE LA RECTA
1. Un negocio adquiere un equipo de cómputo que se deprecia de acuerdo con un modelo lineal. La gráfica ilustra el modelo de depreciación anual.
a) Determine la ecuación de la recta en la forma: general, simétrica y normal.
b) ¿Cuál es el precio inicial del equipo?
c) ¿Cuál es la depreciación anual?
d) ¿Qué significado tiene la pendiente en este caso?
2. La siguiente gráfica muestra el cambio de temperatura que se produce al transferir calor al agua. Determina la ecuación de la recta en cada intervalo indicado en los incisos b, c y d.
a) ¿Que representa la relación de grados por caloría?
b) ¿Cuál es la pendiente del agua en su estado sólido?
c) ¿Cuál es la pendiente del agua en su estado líquido?
d) ¿Cuál es la pendiente del agua en su estado de vapor?
Los puntos A, B, y C son los vértices de un triángulo; para cada una de las siguientes ternas de puntos
1)
A(-2,1), B(4,7), C(6,-3)
Determinar ecuaciones y Trazar
Las mediatrices.
Mediatriz G= x+5y=5
Mediatriz F= -x-y=-5
Mediatriz H= 2x-y=5
Coordenadas del circuncentro= (3.33,1.67)
Mediatriz F= -x-y=-5
Mediatriz H= 2x-y=5
Coordenadas del circuncentro= (3.33,1.67)
Las coordenadas del baricentro: (2.7,1.67)
Las coordenadas del ortocentro: (3.06,1.4)
Las coordenadas del incentro: (2.4,1.71)
Calavera literaria
Calaverita literaria
Estaba Albert Einstein en el CCH, cuando se dirigio al edificio H, en busca del grupo 330 para estudiar Puntos y lineas notables con la maestra Carmen.
Cuando estaba estudiando en el salon todos estaban sorprendidos, hasta que llego la calaca para llevarse de regreso al otro mundo al que la teoria de la relatividad habia creado, todos sorprendidos de lo ocurrido salieron corriendo de la escuela y tomaron un puente de lunes a jueves.
Puntos y lineas notables de un triangulo
Puntos y lineas notables de un triangulo.
Cada triangulo sea rectangulo, equilatero, iscoceles, escaleno etc tiene lineas y puntos notables, mismos que se pueden trazar, algunos son dentro y otros fuera del triangulo.
Lineas
Mediatrices: son las rectas perpendiculares a los lados que dividen a éstos en partes iguales.
Bisectrices: son las rectas que dividen a los ángulos en partes iguales.
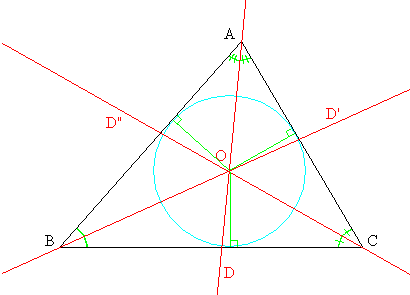
Medianas:son los segmentos que unen los vértices con los puntos medios de los lados opuestos.

Alturas: son los segmentos perpendiculares a los lados (o a la prolongación de éstos) que tienen su otro extremo en el vértice opuesto.

Puntos
Circuncentro: es el punto en el que se encuentran las mediatrices. Este punto no siempre es interior al triángulo.

Incentro: es el punto en el que se encuentran las bisectrices. El incentro es siempre interior al triángulo, de ahí su nombre.
Baricentro: es el punto en el que se encuentran las medianas. En un cuerpo real de forma triangular, el baricentro es el centro de masa (de ahí su nombre, gr. baros = "gravedad"), es decir, el punto desde el cual se puede tomar el cuerpo sin que manifieste tendencia a girar. El baricentro es siempre interior al triángulo.
LA RECTA DE EULER. La recta de Euler de un triángulo es aquella que contiene al Ortocentro, al Circuncentro y al baricentro del mismo. Se llama así en honor al matemático suizo Leonhard Euler, quien descubrió este hecho a mediados del siglo XVIII.
El centro de gravedad es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas porciones materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo. En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo
Cada triangulo sea rectangulo, equilatero, iscoceles, escaleno etc tiene lineas y puntos notables, mismos que se pueden trazar, algunos son dentro y otros fuera del triangulo.
Lineas
Mediatrices: son las rectas perpendiculares a los lados que dividen a éstos en partes iguales.
Bisectrices: son las rectas que dividen a los ángulos en partes iguales.

Medianas:son los segmentos que unen los vértices con los puntos medios de los lados opuestos.
Alturas: son los segmentos perpendiculares a los lados (o a la prolongación de éstos) que tienen su otro extremo en el vértice opuesto.
Puntos
Circuncentro: es el punto en el que se encuentran las mediatrices. Este punto no siempre es interior al triángulo.

Incentro: es el punto en el que se encuentran las bisectrices. El incentro es siempre interior al triángulo, de ahí su nombre.
Baricentro: es el punto en el que se encuentran las medianas. En un cuerpo real de forma triangular, el baricentro es el centro de masa (de ahí su nombre, gr. baros = "gravedad"), es decir, el punto desde el cual se puede tomar el cuerpo sin que manifieste tendencia a girar. El baricentro es siempre interior al triángulo.
Ortocentro: es el punto de encuentro de las alturas. Este punto no siempre es interior al triángulo.
LA RECTA DE EULER. La recta de Euler de un triángulo es aquella que contiene al Ortocentro, al Circuncentro y al baricentro del mismo. Se llama así en honor al matemático suizo Leonhard Euler, quien descubrió este hecho a mediados del siglo XVIII.
Centro de gravedad.
El centro de gravedad es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas porciones materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo. En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo
martes, 20 de septiembre de 2016
Mapas de localización.
Introducción teórica
Cartografía:
Es la ciencia que se encarga de reunir y analizar medidas y datos de regiones de la Tierra, para representarlas gráficamente a diferentes dimensiones lineales escala reducida. Por extensión, también se denomina cartografía a un conjunto de documentos territoriales referidos a un ámbito concreto de estudio.
Los diversos tipos de mapas en la cartografia son:
- General y cartografia tematica:La Cartografía general implica esos mapas que se construyen para una audiencia general y contengan así una variedad de características. Los mapas generales exhiben muchos referencia y los sistemas de localización se producen a menudo en series. La Cartografía temática implica los mapas de temas geográficos específicos, orientados hacia las audiencias específicas. Un par de ejemplos puede ser el mapa del punto demostrar la producción del maíz en Indiana o un mapa sombreado del área de los condados de Ohio, dividido en clases numéricas.
- Topografico y topologico: El mapa topográfico se trata sobre todo de la descripción topográfica de un lugar, incluyendo (especialmente en el Siglo XX) el uso de líneas de isolíneas para demostrar la elevación. El relieve terrestre o relevación se puede demostrar en una variedad de maneras.
Importancia de los mapas:
Desde siempre el ser humano ha tenido la necesidad de conocer el lugar donde vive, la zona en la que se mueve por eso. Por eso ha tenido la necesidad de representar por escrito, mediante dibujos, el espacio que conoce. En principio los mapas son representaciones a escala de un territorio. Actualmente los hay de varios tipos: políticos, físicos, políticos etc.
Toda la información que aportan los mapas son esenciales para muchas de las acciones que un país realiza dentro de su propio territorio, así como para conocimiento de los ejércitos, expedicionarios, o cualquier tipo de persona que lo necesite para un interés particular.
Mapasde localizacion:
CCH ORIENTE A CCH SUR
2 RUTAS EN COCHE
Unidades de medida de un ángulo
MARCO TEÓRICO
Concepto angulo:
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radian, el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas o curvas.
El angulo es la figura formada por dos líneas con origen común. El ángulo entre dos curvas es el ángulo que forman sus rectas tangentes en el punto de intersección
Forma trigonométrica: Es la amplitud de rotación o giro que describe un segmento rectilíneo en torno de uno de sus extremos tomado como vértice desde una posición inicial hasta una posición final.
Un angulo se puede medir en 2 sentidos en positivo y negativo, esto depende de como este ubicado la circunferencia o el segmento de la circunferencia en un plano cartesiano

Las unidades utilizadas para la medida de los ángulos del plano son:
- Radian (usado oficialmente en el Sistema Internacional de Unidades)
- Grado sexagesimal
- Grado centesimal
-
- Introduccion teorica :
-
Suscribirse a:
Entradas (Atom)





























